Derived Value for a Universal Gravitation Constant for Pushing Gravity
Assumptions
- Gravity comes from outer space and pushes.
- Gravity is streams of particles travelling in straight lines.
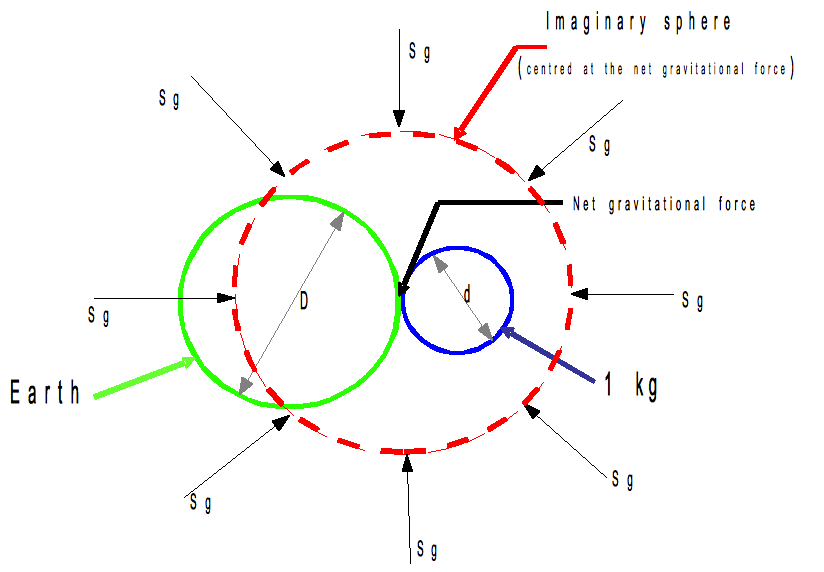

Taking the earth as a sphere and placing a sphere of 1kg mass on the earth's surface, the centre of the imaginary sphere is where the two spheres touch and gravity from one side of the imaginary sphere minus gravity from the other side = net gravitational force.
| Let: | ||
| Sg | = | force of gravity from outer space on unit mass |
| ρ | = | mean earth density = 5514.736kg/m3 |
| D | = | mean diameter of earth = 12742000m |
| d | = | diameter in metres of 1kg |
| kgf | = | force in Newtons of 1kg at the surface of the mean density earth and mean diameter earth at the pole and defined as 9.822604659N which is equal to G x 1kg x earth mass / (earth mean radius)2 |
| G | = | Newtonian universal gravitational constant (6.6743 x 10-11N m2/kg2) |
| Gp | = | effectivity on bulk material |
| SR | = | shielding ratio |
SR is the ratio of shielded space gravity force to unshielded space gravity force passing through the imaginary sphere. The imaginary sphere whose surface passes through the centre of the earth will have gravity streams coming from space through its surface, but a proportion is affected by the earth. This proportion divided by the space gravity through an unaffected sphere is the "shielding ratio". Any gravity stream though, that is not parallel to a line between the earth centre and the net gravitational force position will have a diminishing force in that plane as the angle between the gravity stream and the line from earth to net gravitational force position increases to 90 degrees.
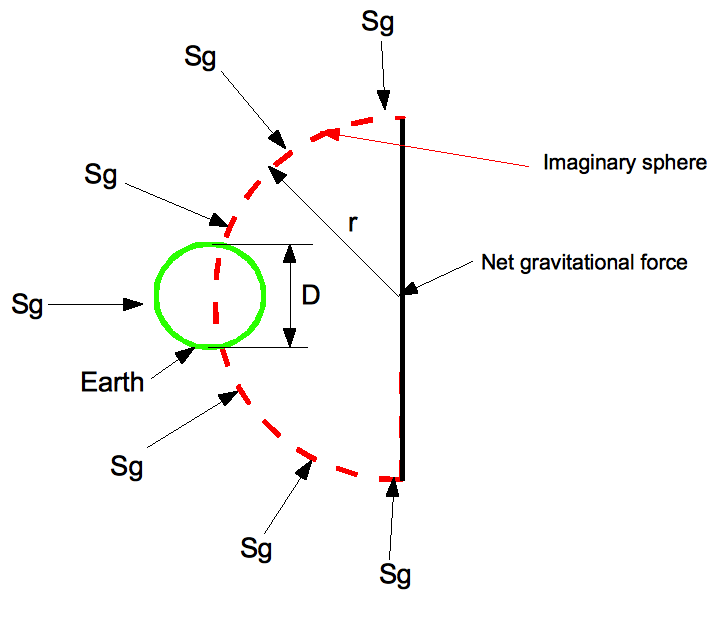
It is well known that the average line length of lines through a circle from a point on its circumference is 2/3 of the diameter, and the average length to the perpendicular from the circumference is 2/3 of the diameter. The value for SR that applies in all cases can be found by moving the centre of the earth to a distance r from where the net gravitational force is to be calculated. If this is made very large in relation to the earth's diameter the streams of particles passing through the earth to where the net gravitational force is measured can be assumed to be parallel to each other.
| Gravitational force shielding | = | cross sectional area of earth times 2/3 |
| = | (D2Π)/6 |
Unshielded gravitational force passing through the imaginary hemisphere is equal to the surface area of a hemisphere with an average effective r in a particular direction. This can be written as:
| (4Πr2)/3 |
This is equivalent to the net force of gravity from the hemisphere surface to the net gravitational force position.
| Therefore | ||||
| SR | = | [(D2GpΠ)/6]/[(4ΠGpr2)/3] | ||
| = | (D2/8r2Π)/6 | (1) | ||
This equation is also derived when the net gravitational force is at the surface of the earth, in this case SR is equal to 0.5 since r is D/2. It will be seen that this relationship applies to any planet or object diameter and its distance from the net gravitational force.
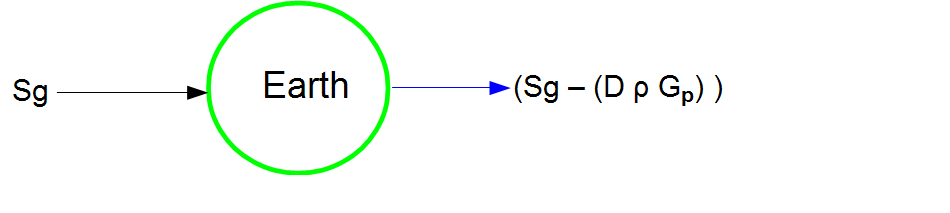
If a stream of gravity particles hit the surface of the earth and pass through it, the amount of force lost by the stream in passing through the earth's diameter is defined as:
| Earths density x distance through earth x the effectivity |
The force in any particular direction is the sum of all the forces with forces perpendicular to the particular direction having no effect.
| net force | = | sum of all forces |
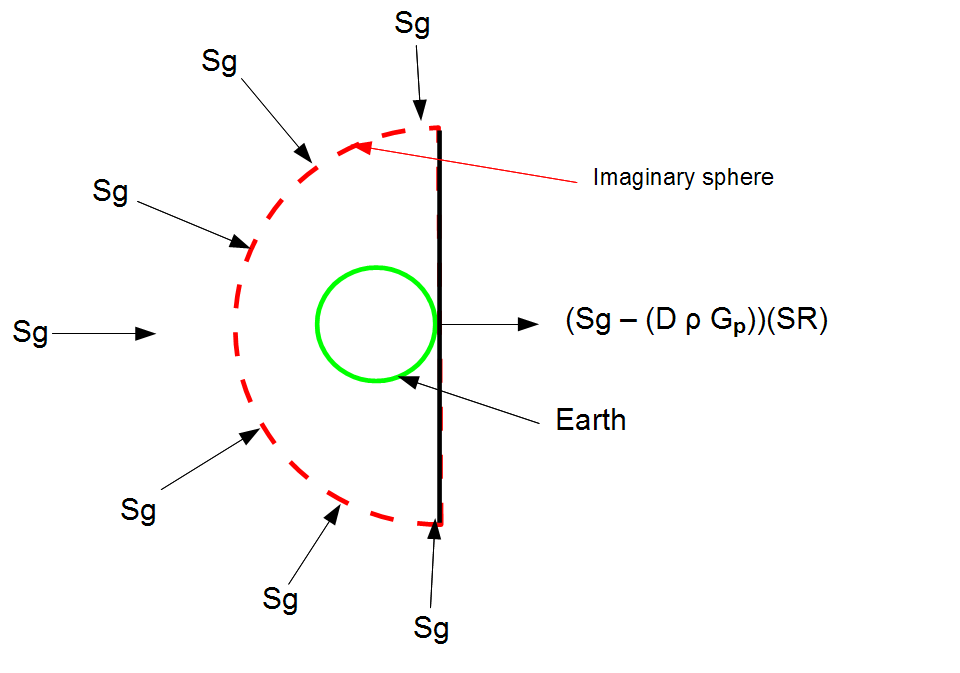
With reference to Figure 1 gravity from one side of the imaginary sphere minus gravity from the other = net gravitational force.
| With d on the surface of D: | ||||
| the force per kg | = | [Sg - (dρGp)SR] - [Sg - (DρGp)SR] | (2) | |
| re-arranging | ||||
| = | [Sg - (dρGp)SR - Sg + (DρGp)SR] | (3) | ||
| simplifying (3) | ||||
| = | [(DρGp)SR - (dρGp)SR] | (4) | ||
| when force = 1kgf then d is negligible relative to D and therefore | ||||
| DρGpSR | = | 1kgf/kg | (5) | |
From (1)
| When r = D/2 ie. net gravitational force is on the surface of D then SR = 0.5 | ||||
| Putting SR = 0.5 into (5) and putting 1kgf = 9.822604659N | ||||
| Gp | = | 2x9.822604659/(Dρ) | (6) | |
If gravity comes from an infinite distance to a point, the number of force lines in a sphere will be constant and with a constant effectivity for any 1kg mass then GpNm2/kg per kg is constant
| Gp | = | 2.795724246x10-10Nm2/kg2 | (7) |
The net gravitational force per kg of an object r distance from the earth's centre is given by combining (1) and (5) and using Gp
| D2GpρD/(8r2) | = | force per kg | (8) |
In general terms
| Let: | ||||
| M1 | = | mass at the net gravitational force (kg) | ||
| D0 | = | diameter of object creating a net gravitational force (m) | ||
| ρ | = | density of object creating a net gravitational force (kg/m3) | ||
| r0 | = | distance between center of M1 and centre of D0(m) | ||
| Then (8) becomes | ||||
| Force | = | (ρD02M1GpD0)/8r02 | (9) | |
Comparing Newton's formula for gravitational force with the one derived above gives a derived value for G.
| From Newton | ||||
| Force F | = | M1M2G/r2 | (10) | |
| where M1 = 1kg | ||||
| F | = | gravitational force of 1kg on the surface of a mean diameter and density of earth at the pole | ||
| r | = | distance between M1 and M2 centres | ||
| earth mass M2 | = | (D3Πρ)/6 | (11) | |
| where D = mean diameter of earth | ||||
| and ρ = mean density of earth | ||||
| Also from (9) | ||||
| F | = | (ρD3M1Gp)/8r2 | ||
| equating (9) and (10) and using (11) | ||||
| (M1ΠρD3G)/6r2 | = | (ρD3M1Gp)/8r2 | ||
| rearranging | ||||
| G | = | 3Gp/4Π | ||
| = | 6.6743x10-11Nm2/kg2 | |||
| Therefore the derived value for Newton's universal gravitation constant is: | ||||
| G | = | 6.6743x10-11Nm2/kg2 | ||
Newton's attractive (pulling) force between two spheres M1 and M2 separated by distance r is given by Force = M1M2G/r2
The force pushing the same two spheres together is given by:
| Force | = | M1Gp(ρD3/8r2) |
| where D is the diameter of M2 and D3 is D2 times the length of D which in the case of a sphere is D but in the case of a spiral galaxy is the combined length of the stars in a column. | ||

| If M1 and M2 are both spheres r distance apart then: | ||
| M1Gp(ρD3/8r2) | = | M1M2G/r2 |
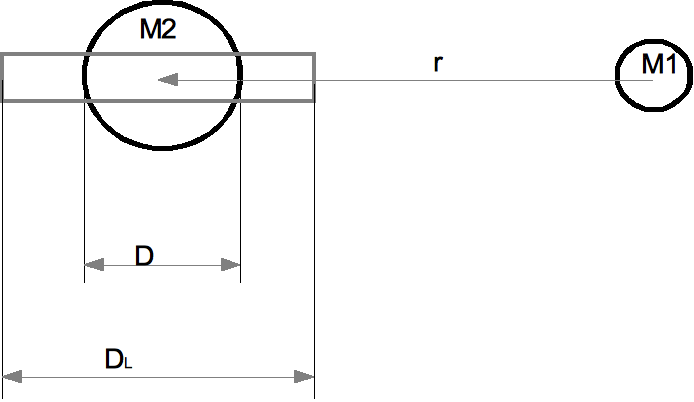
The force on a body at the extremity of a spiral galaxy is influenced by the diameter, density and length of all the bodies in a radial line passing through the imaginary sphere. The sphere can be centred on the extreme body location and the radius is the length to the centre of the galaxy and the length through the galaxy is the length through the column of stars (DL). This will give a force towards the galaxy centre which is more than calculated by Newtonian calculations. The orbital velocity of stars is likely to remain fairly constant since
| centripetal force | = | Mass x velocity2/radius |
and as the radius increases the mass of the line or column of stars increases.
| From equation (9) | ||
| Force | = | (ρD02M1GpD0)/8r02 |
| and for a spiral galaxy it becomes | ||
| Force | = | (ρD02M1GpDL)/8r02 |
| where DL is the summed length of all the stars in the column. | ||
Considering the gravitational force on the earth caused by the sun, both equation (9) and (10) are in agreement except in one case gravity is pushing and in the other it's pulling. Assuming gravity is pushing and comparing (9) with the standard equation for centripetal force F = Mω2r, the mean centripetal force is 0.0007% less than the gravitational force.
If gravity comes from outer space it may be wholly or partly produced in stars. To make up the difference between the centripetal and gravitational force, the sun would need to produce a force of 1.7814 x 10-8N per kg of mass. Gravity produced in the sun will diminish with the square of the distance from the sun. The effect of the sun's gravity on a space probe sent from earth would reduce the probe's acceleration in the direction of the sun by 2.7834 x 10-12m/s2 at 80AU distance from the sun. A further consequence of this reasoning is that if the sun had its mass increased with constant density a point would be reached when the gravity coming out of the sun equalled the gravity coming from outer space. At this point when the sun's net surface gravity force would be zero, the sun would have a mass of 7.03241 x 1039kg. If production of gravity is also dependent on the temperature of the star, cooler bodies collecting under space gravitational force could have a greater mass than could be sustained after warming up by compression and nuclear reactions. This suggests singularities could occur on the galactic scale and also the universal scale.
At the atomic scale the passage of gravity through the nucleus of an atom may be very different from passage through bulk material.
| From equation (6) |
| Gp is constant at 2.795724246x10-10Nm2/kg2 |
On the atomic scale the constant may increase in magnitude from Gp to GpA. Calculations for electron velocity and energy, and the corresponding forces at the principle quantum number, are shown to be balanced by forces from equation (9) if Gp is changed to GpA and
| GpA | = | 6.354783124x1029Nm2/kg2 |
If the gravity particle stream mass rate is equal to the electron orbital mass rate the gravity particle velocity is 6.59 x 1014 x c (where c = speed of light). Feynman found that over the past 200 years there had been several attempts to show that gravity pushed, but the retardation forces on the earth in its orbit around the sun associated with these proposals would have a far greater effect than that which is observed.
In the present case though, the constant associated with atomic forces is GpA and on bulk matter Gp. Using GpA, a minimum for the product of gravity mass (gm) and change in gravity velocity (gvel) can be found which will balance the atomic forces, and from that the minimum change in gvel can be found if it is assumed that the gravity mass rate is equal to the elementary particle mass rate in a given time. The centripetal force of an orbiting mass secured in orbit by a tie or arm is effectively secured by the interaction of the atoms in the tie and this is the same interaction as gravity with elementary particles.
If the gravity mass rate balances the atomic forces at any point in time, then half the earth mass will face forwards and half rearwards and the gravity mass rate will equal the earth mass rate.
The earth's velocity though space is negligible compared to the postulated speed of gravity and results in no reduction in earth's velocity.
This gives a time for the earth to be absorbed by the sun that is longer than the generally accepted length of time for this to happen due to other considerations. The above reasoning shows that all known gravitational forces can be calculated if gravity is a pushing force. If gravity is produced in stars, cold condensed matter may shed matter progressively in ripples as it warms up, a galactic mass could be sufficient for this process. This could also explain the big bang singularity.
For more information, please e-mail info@gravitypushing.org